Answer:
Closed and Bounded.
Explanation:
Hi there!
1) Let's start by finding the values in which the function is defined. Remember that this can be rewritten:
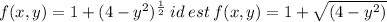
Since every quadratic root are defined for values
 0 then, this help us to understand that we need calculate what interval this Domain is:
0 then, this help us to understand that we need calculate what interval this Domain is:
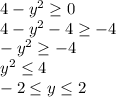
![D=[-2,2]](https://img.qammunity.org/2021/formulas/mathematics/college/jrlgaeokenhja2qjjoy96yq2y69b77kp9c.png)
2) Graphically speaking, the domain is closed. For the values -2 and 2 are included, and bounded.
Bounded functions have all of their points contained by some circle origin centered. Check it out below.