Answer:
The probability that demand during lead-time will exceed 20 bails is 0.2033.
Explanation:
We are given that it has been previously determined that demand during the lead-time is normally distributed with a mean of 15 bails and a standard deviation of 6 bails.
Let X = demand during the lead-time
So, X ~ Normal(
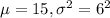 )
)
The z-score probability distribution for the normal distribution is given by;
Z =
 ~ N(0,1)
~ N(0,1)
where,
 population mean demand = 15 bails
population mean demand = 15 bails
 = standard deviation = 6 bails
= standard deviation = 6 bails
Now, the probability that demand during lead-time will exceed 20 bails is given by = P(X > 20 bails)
P(X > 20 bails) = P(
 >
>
 ) = P(Z > 0.83) = 1 - P(Z
) = P(Z > 0.83) = 1 - P(Z
 0.83)
0.83)
= 1 - 0.7967 = 0.2033