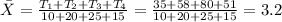Answer:
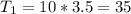

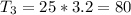

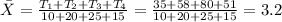
Explanation:
For this case we have the following info given:
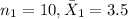 for freshmen
for freshmen
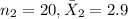 for sophomores
for sophomores
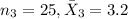 for juniors
for juniors
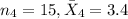 for seniors
for seniors
For this case we can use the formula for the sample mean in order to find the total of each group:
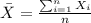
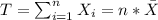
And replacing we got:
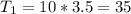

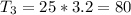

And the grand mean would be given by: