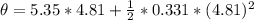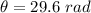Answer:
The angular displacement is
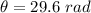
Step-by-step explanation:
From the question we are told that
The initial angular speed is
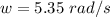
The angular acceleration is
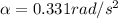
The time take is
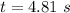
Generally the angular displacement is mathematically represented as
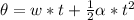
substituting values