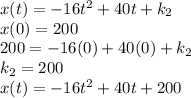Answer:
Initial Value Problem:
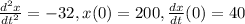
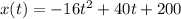
Explanation:
The ball is thrown vertically downward, this means that acceleration due to gravity,
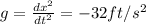
The height of the ball at time, t = 0 at the top of the building will be:
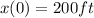
The velocity at which the ball is thrown from the top of the building,

Therefore the initial value problem is written below:
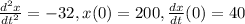
Let us solve for x(t)
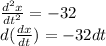
Integrate both sides
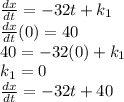
Integrate both sides