Question

Two cars collide at an icy intersection and stick together afterward. The first car has a mass of 1200 kg and was approaching at 6.00 m/s due south. The second car has a mass of 900 kg and was approaching at 25.0 m/s due west. (a) Calculate the final velocity (magnitude in m/s and direction in degrees counterclockwise from the west) of the cars. (Note that since both cars have an initial velocity, you cannot use the equations for conservation of momentum along the x-axis and y-axis; instead, you must look for other simplifying aspects.) magnitude m/s direction ° counterclockwise from west (b) How much kinetic energy (in J) is lost in the collision? (This energy goes into deformation of the cars.) J

Answer 1

a) v = 11.24 m / s , θ = 17.76º b) Kf / K₀ = 0.4380

Step-by-step explanation:

a) This is an exercise in collisions, therefore the conservation of the moment must be used

Let's define the system as formed by the two cars, therefore the forces during the crash are internal and the moment is conserved

Recall that moment is a vector quantity so it must be kept on each axis

X axis

initial moment. Before the crash

p₀ₓ = m₁ v₁

where v₁ = -25.00 me / s

the negative sign is because it is moving west and m₁ = 900 kg

final moment. After the crash

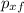`p_(x f)`= (m₁ + m₂) vx

p₀ₓ = p_{x f}

m₁ v₁ = (m₁ + m₂) vₓ

vₓ = m1 / (m₁ + m₂) v₁

let's calculate

vₓ = - 900 / (900 + 1200) 25

vₓ = - 10.7 m / s

Axis y

initial moment

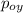`p_(oy)`= m₂ v₂

where v₂ = - 6.00 m / s

the sign indicates that it is moving to the South

final moment

p_{fy}= (m₁ + m₂)
`v_(y)`

p_{oy} = p_{fy}

m₂ v₂ = (m₁ + m₂) v_{y}

v_{y} = m₂ / (m₁ + m₂) v₂

we calculate

`v_(y)` = 1200 / (900+ 1200) 6

`v_(y)` = - 3,428 m / s

for the velocity module we use the Pythagorean theorem

v = √ (vₓ² + v_{y}²)

v = RA (10.7²2 + 3,428²2)

v = 11.24 m / s

now let's use trigonometry to encode the angle measured in the west clockwise (negative of the x axis)

tan θ =
`v_(y)` / Vₓ

θ = tan-1 v_{y} / vₓ)

θ = tan -1 (3,428 / 10.7)

θ = 17.76º

This angle is from the west to the south, that is, in the third quadrant.

b) To search for loss of the kinetic flow, calculate the kinetic enegy and then look for its relationship

Kf = 1/2 (m1 + m2) v2

K₀ = ½ m₁ v₁² + ½ m₂ v₂²

Kf = ½ (900 + 1200) 11.24 2

Kf = 1.3265 105 J

K₀ = ½ 900 25² + ½ 1200 6²

K₀ = 2,8125 10⁵ + 2,16 10₅4

K₀ = 3.0285 105J

the wasted energy is

Kf / K₀ = 1.3265 105 / 3.0285 105

Kf / K₀ = 0.4380

this is the fraction of kinetic energy that is conserved, transforming heat and transforming potential energy