Answer:
The intensity of the beam 16 feet below the surface is 0.06% of the initial intensity of the incident beam.
Explanation:
"When a vertical beam of light passes through a transparent medium, the rate at which its intensity I decreases is proportional to I(t), where t represents the thickness of the medium (in feet).
This means that the intersity can be modeled by the following differential equation:
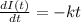
In which k is the decrease rate.
This differential equation leads to the following solution:
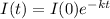
In which I(0) is the initial intensity.
The intensity 3 feet below the surface is 25% of the initial intensity I0 of the incident beam.
This means that I(3) = 0.25I(0). We use this to find k. So
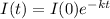
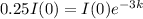
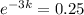
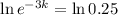
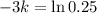

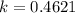
So
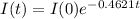
What is the intensity of the beam 16 feet below the surface
This is I(16). So
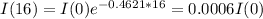
The intensity of the beam 16 feet below the surface is 0.06% of the initial intensity of the incident beam.