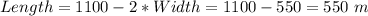Question

A rectangular plot of farmland will be bounded on one side by a river and on the other three sides by a​ single-strand electric fence. With 1100 m of wire at your​ disposal, what is the largest area you can​ enclose, and what are its​ dimensions?

Answer 1

Length = 550 m

Width = 275 m

Area = 151,250 m2

Explanation:

One side of the farmland is bounded by the river, so the perimeter we will need to enclose is:

`Perimeter = Length + 2*Width = 1100\ m`

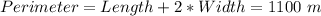
And the area of the farmland is given by:

`Area = Length * Width`

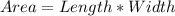
From the Perimeter equation, we have that:

`Length = 1100 - 2*Width`

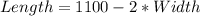
Using this in the area equation, we have:

`Area = (1100 - 2*Width) * Width`

`Area = 1100*Width - 2*Width^2`

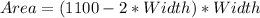
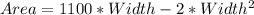
Now, to find the largest area, we need to find the vertex of this quadratic equation, and we can do that using the formula:

`Width = -b/2a`

`Width = -1100/(-4)`

`Width = 275\ m`

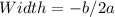
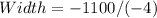
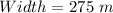
This width will give the maximum area of the farmland. Now, finding the length and the maximum area:

`Length = 1100 - 2*Width = 1100 - 550 = 550\ m`

`Area = Length * Width = 550 * 275 = 151250\ m2`