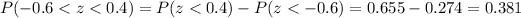Question

The weights of college football players are normally distributed with a mean of 200 pounds and a standard deviation of 50 pounds. If a college football player is randomly selected, find the probability that he weighs between 170 and 220 pounds.

Answer 1

`P(170<X<220)=P((170-\mu)/(\sigma)<(X-\mu)/(\sigma)<(220-\mu)/(\sigma))=P((170-200)/(50)<Z<(220-200)/(50))=P(-0.6<z<0.4)`

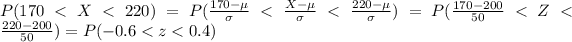
And we can find this probability with this difference:

`P(-0.6<z<0.4)=P(z<0.4)-P(z<-0.6)=0.655-0.274= 0.381`

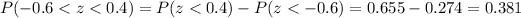
Explanation:

Let X the random variable that represent the weights of a population, and for this case we know the distribution for X is given by:

`X \sim N(200,50)`

Where
`\mu=200` and
`\sigma=50`

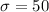
We want to find the following probability:

`P(170<X<220)`

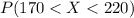
And we can use the z score formula given by:

`z=(x-\mu)/(\sigma)`

And using this formula we got:

`P(170<X<220)=P((170-\mu)/(\sigma)<(X-\mu)/(\sigma)<(220-\mu)/(\sigma))=P((170-200)/(50)<Z<(220-200)/(50))=P(-0.6<z<0.4)`

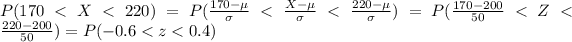
And we can find this probability with this difference:

`P(-0.6<z<0.4)=P(z<0.4)-P(z<-0.6)=0.655-0.274= 0.381`