Answer:
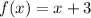
Explanation:
Given
Points (−5,−2) and (−3,0)
Required
Find a linear function that passes through the given points
The question implies that we solve for the equation for the line;
First, the slope of the line must be calculated;
This is calculated as thus:

Where
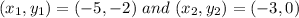
So,
 becomes
becomes

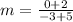
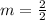
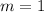
The equation of the line can then be calculated using any of the given points;
Using

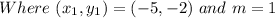
We have

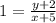
Multiply both sides by x + 5
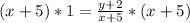
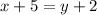
Subtract 2 from both sides
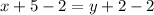
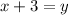
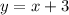
Replace y with f(x)
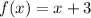
Hence, from the list of given options; Option B is correct