Question

Given A triangle with sides x=6.35 cm and Y=12.25 cm with an angle of 90 degrees between them, find the length of the hypotenuse and the size of the other two angles.

Answer 1

Hypotenuse = 13.798 cm, Angle1 = 27.4° and Angle2 = 62.59°

Explanation:

The first step to help us understand the question would be to draw it out.

A right angled triangle, with the two sides that make the right angle being x and y (it does not matter which way you put x and y).

I have attached the quick sketch I will refer to.

To find the length of the hypotenuse (lets call it H) we can use Pythagoras theorem as shown below

`{x^(2)+y^(2)} = H^(2)`

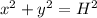
Substitute in our values for x and y, and solve for H

`{6.35^(2)+12.25^(2)} = H^(2)`

`190.385 = H^(2)`

`√(190.385) = H`

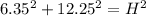
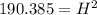
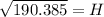
H = 13.79 cm

To find the other two angles of the triangle we will use trigonometry

I will first look for angle ∅. Since we have all three sides of the triangle we can use any of the three trig functions, I chose to use Tan

Tan ∅
`= (opposite)/(adjacent)`

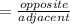
Substitute in our values for x and y, and solve for ∅

Tan ∅ =
`(6.35)/(12.25)`

∅ =
`tan^(-1) (6.35)/(12.25)`

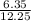
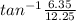
∅ = 27.4°

Now do the same for angle β. I chose to use Tan again

Tan β
`= (opposite)/(adjacent)`

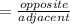
Substitute in our values for x and y, and solve for β

Tan β =
`(12.25)/(6.35)`

β =
`tan^(-1) (12.25)/(6.35)`

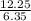
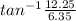
β = 62.59°