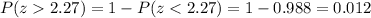Answer:

And we can find this probability using the z score formula and the complement rule and we got:
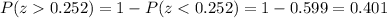

And we can find this probability using the z score formula and the complement rule and we got:
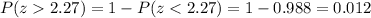
Explanation:
Let X the random variable that represent the SAT scores of a population, and for this case we know the distribution for X is given by:
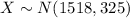
Where
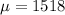 and
and
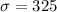
We want to find this probability:
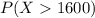
And we can use the z score formula given by:

Using this formula we got:

And we can find this probability using the z score formula and the complement rule and we got:
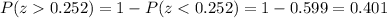
For the other part we need to take in count that the distribution for the sampel mean if the sample size is large (n>30) is given by:

And we can use the z score formula given by:
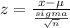
And replacing we got:

And we can find this probability using the z score formula and the complement rule and we got: