Question

At which root does the graph of f(x) = (x – 5)3(x + 2)2 touch the x-axis?

-5
-2
Ο Ο Ο Ο
2
5

Answer 1

At x = -2 the graph of this polynomial will touch the x-axis.

Explanation:

Recall the behavior difference between power functions of even and odd power. Odd powers are associated with the crossing of the x-axis, while even powers are associated with "touching" of the x axis.

in this cases, since they give you the function in factor form, the actual roots (x-values where the function adopts value zero) of the function are evident :

`f(x)=(x-5)^3\, (x+2)^2`

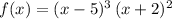
It has a root at x = 5 [notice that at such x-value the factor (x-5) becomes zero], and this root is of multiplicity "3" (given by the power associated with the binomial factor for this root)

and has another root at x = -2 [notice that at such x-value the factor (x+2) becomes zero], and this root is of multiplicity "2" (given by the power associated with the binomial factor for it)

It is just the second root analyzed the one that shows an even power (2) associated to its binomial factor, and therefore it is at x= -2 that the graph of this function will show as "touching" the x axis.