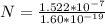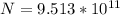Question

A spherical conductor with a 0.193 m radius is initially uncharged. How many electrons should be removed from the sphere in order for it to have an electrical potential of 7.10 kV at the surface?

Answer 1

The number of electrons removed is
`N = 9.513 *10^(11)`

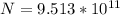
Step-by-step explanation:

From hr question we are told that

The radius is
`r = 0.193 \ m`

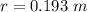
The required electrical potential is
`V = 7.10 \ kV = 7.10 *10^(3) V`

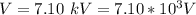
The total charge on the sphere is mathematically evaluated as

`Q = (Vr)/(k)`

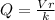
where k is the coulombs constant with value
`k =9)*10^(9) \ kg\cdot m^3\cdot s^(-4)\cdot A^2.`

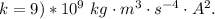
substituting value

`Q = (7.10 *10^3 * 0.193)/(9*10^9)`

`Q = 1.522*10^(-7) C`

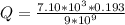
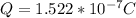
The number of electron removed is mathematically evaluated as

`N = (Q)/(e)`

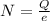
Where e is the charge on one electron with value
`e = 1.6 *10^(-19) \ C`

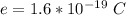
substituting values

`N = (1.522 *10^(-7))/(1.60*10^(-19))`

`N = 9.513 *10^(11)`