Question

The average age of residents in a large residential retirement community is 69 years with standard deviation 5.8 years The probability that the average age, xbar of the 100 residents selected is less than 68.5 years is:

Answer 1

The probability that the average of the 100 residents selected is less than 68.5 years is

P( x⁻< 68.5) = 0.1949

Explanation:

Step(i):-

Given mean of the Population = 69

Given standard deviation of the Population = 5.8 years

Let x⁻ be the average random variable in normal distribution

Given x⁻ = 68.5

By using

`Z = (x^(-)-mean )/((S.D)/(√(n) ) )`

`Z = (68.5-69 )/((5.8)/(√(100) ) )`

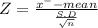
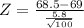
Z = -0.862

Step(ii):-

The probability that the average of the 100 residents selected is less than 68.5 years is

P( x⁻< 68.5) = P( z <-0.862)

= 1- P( Z >- 0.862)

= 1 - ( 0.5 + A(-0.862)

= 0.5 - A( 0.862) ( A( -Z) = A(Z))

= 0.5 - 0.3051

= 0.1949

Conclusion:-

The percentage of the probability that the average of the 100 residents selected is less than 68.5 years = 19 %