Question

The 2003 Zagat Restaurant Survey provides food, decor, and service ratings for some of the top restaurants across the United States. For 15 top-ranking restaurants located in Boston, the average price of a dinner, including one drink and tip, was $48.60. You are leaving on a business trip to Boston and will eat dinner at three of these restaurants. Your company will reimburse you for a maximum of $50 per dinner. Business associates familiar with the restaurants have told you that the meal cost at 5 of the restaurants will exceed $50. Suppose that you randomly select three of these restaurants for dinner.

Required:
a. What is the probability that none of the meals will exceed the cost covered by your company?
b. What is the probability that one of the meals will exceed the cost covered by your company?
c. What is the probability that two of the meals will exceed the cost covered by your company?
d. What is the probability that all three of the meals will exceed the cost covered by your company?

Answer 1

a. P(x=0)=0.2967

b. P(x=1)=0.4444

c. P(x=2)=0.2219

d. P(x=3)=0.0369

Explanation:

The variable X: "number of meals that exceed $50" can be modeled as a binomial random variable, with n=3 (the total number of meals) and p=0.333 (the probability that the chosen restaurant charges mor thena $50).

The probabilty p can be calculated dividing the amount of restaurants that are expected to charge more than $50 (5 restaurants) by the total amount of restaurants from where we can pick (15 restaurants):

`p=(5)/(15)=0.333`

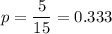
Then, we can model the probability that k meals cost more than $50 as:

`P(x=k) = \dbinom{n}{k} p^(k)(1-p)^(n-k)\\\\\\P(x=k) = \dbinom{3}{k} 0.333^(k) 0.667^(3-k)\\\\\\`

a. We have to calculate P(x=0)

`P(x=0) = \dbinom{3}{0} p^(0)(1-p)^(3)=1*1*0.2967=0.2967\\\\\\`

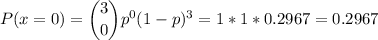
b. We have to calculate P(x=1)

`P(x=1) = \dbinom{3}{1} p^(1)(1-p)^(2)=3*0.333*0.4449=0.4444\\\\\\`

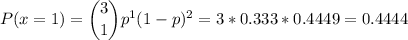
c. We have to calcualte P(x=2)

`P(x=2) = \dbinom{3}{2} p^(2)(1-p)^(1)=3*0.1109*0.667=0.2219\\\\\\`

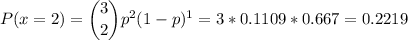
d. We have to calculate P(x=3)

`P(x=3) = \dbinom{3}{3} p^(3)(1-p)^(0)=1*0.0369*1=0.0369\\\\\\`