Question

Your father is 50 years old and will retire in 10 years. He expects to live for 25 years after he retires, until he is 85. He wants a fixed retirement income that has the same purchasing power at the time he retires as $60,000 has today. (The real value of his retirement income will decline annually after he retires.) His retirement income will begin the day he retires, 10 years from today, at which time he will receive 24 additional annual payments. Annual inflation is expected to be 5%. He currently has $105,000 saved, and he expects to earn 8% annually on his savings. The data has been collected in the Microsoft Excel Online file below. Open the spreadsheet and perform the required analysis to answer the question below.How much must he save during each of the next 10 years (end-of-year deposits) to meet his retirement goal?

Answer 1

It will need $ 107,120.321 dolalr per year to achieve his retirement goal

Step-by-step explanation:

We first must calcualte the prsent value of the 25 payments with equal worth of 60,000 dollar of today.

First we move the 60,000 forward 10 years

`Principal \: (1+ r)^(time) = Amount`

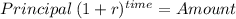
Principal 60,000.00

time 10.00

rate 0.05000

`60000 \: (1+ 0.05)^(10) = Amount`

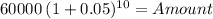
Amount 97,733.68

Now, we calculate the present value of an annuity considering this 5% inflation

`C_0 * ((1+r)^n-(1+g)^n)/(r-g)  = PV`

g 0.05

r 0.08

C 97,734

n 25

$ 1,778,492.341

Then, decrease this by the amounnt already saved by our father:

`Principal \: (1+ r)^(time) = Amount`

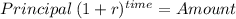
Principal 105,000.00

time 10.00

rate 0.08000

`105000 \: (1+ 0.08)^(10) = Amount`

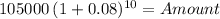
Amount 226,687.12

Additional saving needed:

1,778.492-34 - 226,687.12 = 1.551.805,22

Now, we solve the annual saving to achieve this future value:

`PV / ((1+r)^(time) -1)/(rate) = C\\`

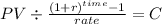
PV 1,551,805.22

time 10

rate 0.08

`1551805.22 / ((1+0.08)^(10) -1)/(0.08) = C\\`

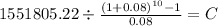
C $ 107,120.321

‬