Answer:
The angular speed of the new system is
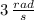 .
.
Step-by-step explanation:
Due to the absence of external forces between both disks, the Principle of Angular Momentum Conservation is observed. Since axes of rotation of each disk coincide with each other, the principle can be simplified into its scalar form. The magnitude of the Angular Momentum is equal to the product of the moment of inertial and angular speed. When both disks begin to rotate, moment of inertia is doubled and angular speed halved. That is:
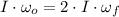
Where:
 - Moment of inertia of a disk, measured in kilogram-square meter.
- Moment of inertia of a disk, measured in kilogram-square meter.
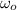 - Initial angular speed, measured in radians per second.
- Initial angular speed, measured in radians per second.
 - Final angular speed, measured in radians per second.
- Final angular speed, measured in radians per second.
This relationship is simplified and final angular speed can be determined in terms of initial angular speed:
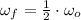
Given that
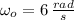 , the angular speed of the new system is:
, the angular speed of the new system is:


The angular speed of the new system is
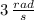 .
.