Question

A Ferris wheel turns at a constant 150.0 revolutions per hour. (a) Express this rate of rotation in units of radians per second. 36.44 Incorrect: Your answer is incorrect. Write the given rate of rotation with its given units, then convert the units to the desired units. rad/s (b) If the wheel has a radius of 13.0 m, what arc length does a passenger trace out during a ride lasting 4.95 min

Answer 1

(a) 0.261 rad/s

(b) 1007.72 m

Step-by-step explanation:

The angular velocity of the Ferris wheel is 150.0 revolutions per hour.

(a) To calculate the angular velocity of the wheel in units of radians per second, you take into account the following equivalence:

1 hour = 3600 seconds

1 revolution = 2π radians

You use the previous conversion factors:

`150.0\ (rev)/(h)*(2\pi \ rad)/(1\ rev)*(1\ h)/(3600\ s)=0.261(rad)/(s)`

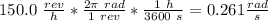
In units of radians per seconds the wheel turns at 0.261 rad/s

(b) To find the arc length described by the wheel, you first calculate the angle described by the wheel in the time t, by using the following formula:

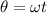`\theta=\omega t` (1)

ω: angular velocity = 0.261 rad/s

t: time = 4.95 min

You first convert the time to units of seconds

`4.95min*(60s)/(1min)=297s`

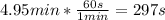
Next, you replace the values of the parameters in the equation (1):

`\theta=(0.261(rad)/(s))(297s)=77.51rad`

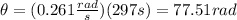
Next, you use the following formula for the arc length:

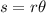`s=r\theta` (2)

r: radius of the wheel = 13.0 m

You replace the values of the parameters in the equation (2):

`s=(13.0m)(77.51rad)=1007.72m`

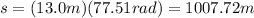
The arc length described by the wheel is 1007.72m