Question

In 1949, an automobile manufacturing company introduced a sports car (the "Model A") which could accelerate from 0 to speed v in a time interval of Δt. In order to boost sales, a year later they introduced a more powerful engine (the "Model B") which could accelerate the car from 0 to speed 2.92v in the same time interval. Introducing the new engine did not change the mass of the car. Compare the power of the two cars, if we assume all the energy coming from the engine appears as kinetic energy of the car.

Answer 1

Answer:
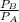`(P_B)/(P_A)` = 8.5264

Explanation: Power is the rate of energy transferred per unit of time: P =
`(E)/(t)`

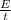
The energy from the engine is converted into kinetic energy, which is calculated as:
`KE = (1)/(2).m.v^(2)`

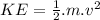
To compare the power of the two cars, first find the Kinetic Energy each one has:

K.E. for Model A

`KE_A = (1)/(2).m.v^(2)`

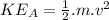
K.E. for model B

`KE_B = (1)/(2).m.(2.92v)^(2)`

`KE_B = (1)/(2).m.8.5264v^(2)`

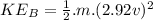
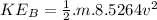
Now, determine Power for each model:

Power for model A

`P_(A)` =
`(m.v^(2) )/(2.t)`

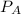Power for model B

`P_B = (m.8.5264.v^(2) )/(2.t)`

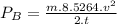
Comparing power of model B to power of model A:

`(P_B)/(P_A) = (m.8.5264.v^(2) )/(2.t).(2.t)/(m.v^(2) )`

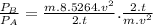
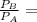`(P_B)/(P_A) =` 8.5264

Comparing power for each model, power for model B is 8.5264 better than model A.