Question

A fuel oil company claims that one-fifth of the homes in a certain city are heated by oil. Do we have reason to believe that fewer than one-fifth are heated by oil if, in a random sample of 1000 homes in this city, 136 are heated by oil? Please show all 4 steps of the classical approach clearly using α = 0.05.

Answer 1

Yes, we have reason to believe that fewer than one-fifth are heated by oil.

Explanation:

A one-sample proportion test is to be performed to determine whether fewer than one-fifth of the homes in a certain city are heated by oil.

The hypothesis can be defined as follows:

H₀: The proportion of homes in a certain city that are heated by oil is not less than one-fifth, i.e. p ≥ 0.20.

Hₐ: The proportion of homes in a certain city that are heated by oil is less than one-fifth, i.e. p < 0.20.

The information provided is:

n = 1000

x = 136

α = 0.05

Compute the sample proportion as follows:

`\hat p=(x)/(n)=(136)/(1000)=0.136`

Compute the test statistic as follows:

`z=\frac{\hat p-p}{\sqrt{(p(1-p))/(n)}}`

`=\frac{0.136-0.20}{\sqrt{(0.136(1-0.136))/(1000)}}\\\\=-5.9041\\\\\approx -5.90`

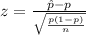
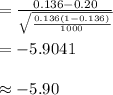
The test statistic value is, -5.90.

Decision rule:

Reject the null hypothesis if the p-value of the test is less than the significance level.

Compute the p-value as follows:

`p-value=P(Z<-5.90)\\\\=1-P(Z<5.90)\\\\=1-(\approx 1)\\\\=0`

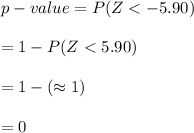
The p-value of the test is, 0.

p-value = 0 < α = 0.05

The null hypothesis will be rejected at 5% level of significance.

Conclusion:

The proportion of homes in a certain city that are heated by oil is less than one-fifth.