Question

A computer manufacturer estimates that its cheapest screens will last less than 2.8 years. A random sample of 61 of these screens has a mean life of 2.4 years. The population is normally distributed with a population standard deviation of 0.88 years. At α=0.02, what type of test is this and can you reject the organization’s claim using the test statistic?

Answer 1

The null and alternative hypotheses:

H0: u = 2.8

H1: u < 2.8

This is a left - tailed test.

For test statistics, use the formula:

`Z = (x' - u)/(\sigma/ √(n))`

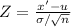
Where,

Mean, u = 2.8

Sample mean,x' = 2.4

Sample size, n = 61

Standard deviation
`\sigma` = 0.88

Significance level = 0.02

`Z = (2.4 - 0.02)/(0.88/ √(61)) =-3.55`

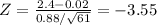
Test statistics, Z = -3.55

Pvalue:

Pvalue of Z = -3.55 using standard normal table,

NORMSTID(-3.55) = 0.00019

Pvalue = 0.0002

Critical value:

Since this is a left tailed test, the critical value at 0.02 level of significance is:

`Z_\alpha = Z_0_._0_2 = -2.05`

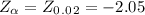
Decision: If pvalue is less than level of significance reject null hypothesis H0.

Conclusion:

Since pvalue, 0.00019 is less than level of significance, 0.02, reject null hypothesis, H0.

We conclude that the mean life of the cheapest screen is less than 2.8 years

Answer 2

The test is left - tailed

We cannot reject the organization's claim ( its cheapest screens will truly last less than 2.8 years)

Explanation:

Sample size, n = 61

Sample mean,
`\bar{X} = 2.4`

Standard deviation,
`\sigma = 0.88`

Significance level, α=0.02

Null hypothesis,
`H_(o) : \mu = 2.8`

Alternative hypothesis,
`H_(a) : \mu < 2.8`

It is clearly seen from the alternative hypothesis, that it is a left tailed test. It is not tailed towards the two directions.

Calculate the test statistic:

`Z = \frac{\bar{X} - \mu}{\sigma/√(n) } \\Z = (2.4 - 2.8)/(0.88/√(61) )\\Z = - 3.55`

Calculate the P-value:

P(Z < -3.35) = 0.0002

Since (p-value = 0.0002) < (α=0.02), the null hypothesis is rejected.

It can therefore be concluded that the mean of the cheapest screen is less than 2.8 years. i.e. the cheapest screen will last less than 2.8 years