Question

A recent research show that only 40% of the customers are willing to pay more for the service. Now we have selected 10 customers randomly. What are the expected value and standard deviation

Answer 1

The expected number of customers that pay more for the service is 4 and the standard deviation is 1.55.

Explanation:

For each customer, there are only two possible outcomes. Either they are willing to pay more for the service, or they are not. Customers are independent. So we use the binomial probability distribution to solve this question.

Binomial probability distribution

Probability of exactly x sucesses on n repeated trials, with p probability.

The expected value of the binomial distribution is:

`E(X) = np`

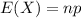
The standard deviation of the binomial distribution is:

`√(V(X)) = √(np(1-p))`

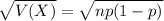
40% of the customers are willing to pay more for the service.

This means that
`p = 0.4`

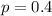
Now we have selected 10 customers randomly.

This means that
`n = 10`

What are the expected value and standard deviation

`E(X) = np = 10*0.4 = 4`

`√(V(X)) = √(np(1-p)) = √(10*0.4*0.6) = 1.55`

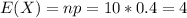
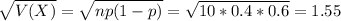
The expected number of customers that pay more for the service is 4 and the standard deviation is 1.55.