Answer:
The coefficients of static and kinetic friction for this experiment are 0.716 and 0.596, respectively.
Step-by-step explanation:
The Free Body Diagram associated with the experiment is presented as attachment included below.
Friction is a contact force that occurs as a reaction against any change in state of motion, which is fostered by gravity.
Normal force is another contact force that appears as a reaction to the component of weight perpendicular to the direction of motion. Let consider a framework of reference consisting in two orthogonal axes, one being parallel to the direction of motion (x-axis) and the other one normal to it (y-axis). Equations of motion are described herein:
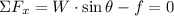
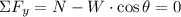
Where:
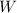 - Weight of the eraser, measured in newtons.
- Weight of the eraser, measured in newtons.
 - Friction force, measured in newtons.
- Friction force, measured in newtons.
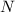 - Normal force, measured in newtons.
- Normal force, measured in newtons.
 - Angle of the incline, measured in degrees.
- Angle of the incline, measured in degrees.
The maximum allowable static friction force is:
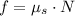
Where:
 - Coefficient of static friction, dimensionless.
- Coefficient of static friction, dimensionless.
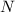 - Normal force, measured in newtons.
- Normal force, measured in newtons.
Likewise, the kinetic friction force is described by the following model:
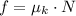
Where:
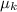 - Coefficient of static friction, dimensionless.
- Coefficient of static friction, dimensionless.
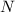 - Normal force, measured in newtons.
- Normal force, measured in newtons.
And weight is equal to the product of the mass of eraser and gravitational constant (
 )
)
In this exercise, coefficients of static and kinetic friction must be determined. First equation of equilibrium has to be expanded and coefficient of friction cleared:
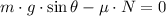

But
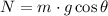 , so that:
, so that:
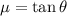
Now, coefficients of static and kinetic friction are, respectively:

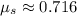
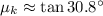
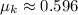
The coefficients of static and kinetic friction for this experiment are 0.716 and 0.596, respectively.