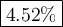Question

A 4 cm diameter "bobber" with a mass of 3 grams floats on a pond. A thin, light fishing line is tied to the bottom of the bobber, and from the bottom hangs a 10 gram lead weight. The density of lead is 11.3 g/cm3. What fraction of the bobber's volume is submerged, as a percent of the total volume

Answer 1

Step-by-step explanation:

Calculate the volume of the lead

`V=(m)/(d)\\\\=(10g)/(11.3g'cm^3)`

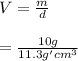
Now calculate the bouyant force acting on the lead

`F_L = Vpg`

`F_L=((10g)/(11.3g/cm^3) )(1g/cm^3)(9.8m/s^2)\\\\=8.673* 10^(-3)N`

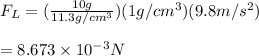
This force will act in upward direction

Gravitational force on the lead due to its mass will act in downward direction

Hence the difference of this two force

`T=mg-F_L\\\\=(10*10^(-3)kg(9.8m/s^2)-8.673* 10^(-3)\\\\=8.933*10^(-3)N`

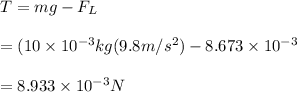
If V is the volume submerged in the water then bouyant force on the bobber is

`F_B=V'pg`

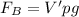
Equate bouyant force with the tension and gravitational force

`F_B=T_mg\\\\V'pg=((8.933*10^(-2)N)+mg)/(pg) \\\\V'=((8.933*10^(-2)N)+mg)/(pg)`

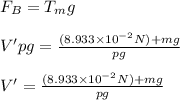
Now Total volume of bobble is

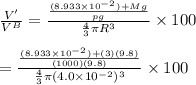
`(V')/(V^B) =(((8.933*10^(-2))+Mg)/(pg) )/((4)/(3) \pi R^3 )*100\\\\=(((8.933*10^(-2))+(3)(9.8))/((1000)(9.8)) )/((4)/(3) \pi (4.0*10^(-2))^3 )*100\\\\`

=
`\large\boxed{4.52 \%}`