Four lines extend from point K. The space between lines K J and K N is 58 degrees. The space between lines K N and K M is 61 degrees. The space between lines K M and K L is 61 d…

Question

asked Mar 1, 2021 38.5k views

1 Answer

Arun Kumar P · Answer 1 · 2021-03-04T16:51:57+0000

Answer:

Ray KM is an angle bisector of
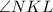$\angle NKL$ .

Explanation:

Given that there are 4 lines that are extended from a point K.

Angle between KJ and KN is
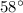$58^\circ$ i.e.
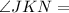
$\angle JKN =$
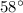
$58^\circ$

Angle between KN and KM is
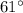$61^\circ$ i.e.
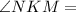
$\angle NKM =$
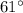$61^\circ$ .

Angle between KM and KL is
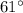$61^\circ$ i.e.
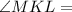
$\angle MKL =$
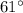
$61^\circ$

Please refer to the attached image for the conditions and dimensions of angles given in the question statement.

Now, let us have a look at the options given:

1. Point K is a midpoint of Line segment JL

JL is not a straight line first of all, and secondly there is no condition given about the line segments.

So, it is incorrect.

2.
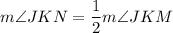
$m \angle JKN = (1)/(2)m \angle JKM$

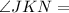
$\angle JKN =$
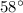$58^\circ$ and

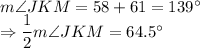
$m \angle JKM =58+61=139^\circ\\\Rightarrow (1)/(2) m \angle JKM = 64.5^\circ$

So, it is also incorrect.

3. Ray KM is an angle bisector of
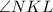$\angle NKL$ .

Ray KM divides the
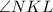$\angle NKL$ into two equal angles
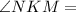
$\angle NKM =$
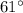$61^\circ$ and
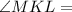
$\angle MKL =$
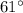$61^\circ$ so it is correct.