Question

Suppose we are interested in bidding on a piece of land and we know one other bidder is interested. The seller announced that the highest bid in excess of $10,400 will be accepted. Assume that the competitor's bid x is a random variable that is uniformly distributed between $10,400 and $15,400.

Required:
a. Suppose you bid $12,000. What is the probability that your bid will be accepted (to 2 decimals)?
b. Suppose you bid $14,000. What is the probability that your bid will be accepted (to 2 decimals)?
c. What amount should you bid to maximize the probability that you get the property (in dollars)?

Answer 1

a) 0.32 = 32% probability that your bid will be accepted

b) 0.72 = 72% probability that your bid will be accepted

c) An amount in excess of $15,400.

Explanation:

An uniform probability is a case of probability in which each outcome is equally as likely.

For this situation, we have a lower limit of the distribution that we call a and an upper limit that we call b.

The probability that we find a value X lower than x is given by the following formula.

`P(X \leq x) = (x - a)/(b-a)`

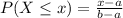
Assume that the competitor's bid x is a random variable that is uniformly distributed between $10,400 and $15,400.

This means that
`a = 10400, b = 15400`

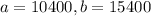
a. Suppose you bid $12,000. What is the probability that your bid will be accepted (to 2 decimals)?

You will win if the competitor bids less than 12000. So

`P(X \leq 12000) = (12000 - 10400)/(15400 - 10400) = 0.32`

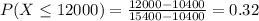
0.32 = 32% probability that your bid will be accepted

b. Suppose you bid $14,000. What is the probability that your bid will be accepted?

You will win if the competitor bids less than 14000. So

`P(X \leq 14000) = (14000 - 10400)/(15400 - 10400) = 0.72`

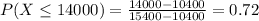
0.72 = 72% probability that your bid will be accepted

c. What amount should you bid to maximize the probability that you get the property (in dollars)?

His bid is uniformly distributed between $10,400 and $15,400.

So, to maximize the probability that you get the property, you should bid an amount in excess of $15,400.