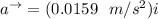Answer:
the acceleration
Step-by-step explanation:
Given that:
the initial speed v₁ = 0 m/s i.e starting from rest ; since the car accelerates at a distance Δx = 6 miles in order to teach that final speed v₂ of 63.15 km/h.
So; the acceleration for the first 6 miles can be calculated by using the formula:
v₂² = v₁² + 2a (Δx)
Making acceleration a the subject of the formula in the above expression ; we have:
v₂² - v₁² = 2a (Δx)
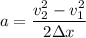
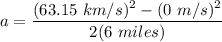
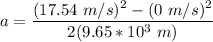
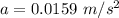
Thus;
Assume the car moves in the +x direction;
the acceleration