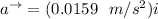Question

In 1898, the world land speed record was set by Gaston Chasseloup-Laubat driving a car named Jeantaud. His speed was 39.24 mph (63.15 km/h), much lower than the limit on our interstate highways today. Repeat the calculations of Example 2.7 (assume the car accelerates for 6 miles to get up to speed, is then timed for a one-mile distance, and accelerates for another 6 miles to come to a stop) for the Jeantaud car. (Assume the car moves in the +x direction.)

Find the acceleration for the first 6 miles.

Answer 1

the acceleration
`a^(\to) = (0.0159 \ \ m/s^2 )i`

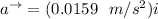
Step-by-step explanation:

Given that:

the initial speed v₁ = 0 m/s i.e starting from rest ; since the car accelerates at a distance Δx = 6 miles in order to teach that final speed v₂ of 63.15 km/h.

So; the acceleration for the first 6 miles can be calculated by using the formula:

v₂² = v₁² + 2a (Δx)

Making acceleration a the subject of the formula in the above expression ; we have:

v₂² - v₁² = 2a (Δx)

`a = (v_2^2 - v_1^2 )/(2 \Delta x)`

`a = ((63.15 \ km/s)^2 - (0 \ m/s)^2 )/(2 (6 \ miles))`

`a = ((17.54 \ m/s)^2 - (0 \ m/s)^2 )/(2 (9.65*10^3 \ m))`

`a =0.0159 \ m/s^2`

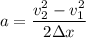
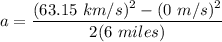
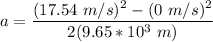
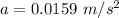
Thus;

Assume the car moves in the +x direction;

the acceleration
`a^(\to) = (0.0159 \ \ m/s^2 )i`