Answer:
the isentropic efficiency of turbine is 99.65%
Step-by-step explanation:
Given that:
Mass flow rate of LNG m = 20 kg/s
The pressure at the inlet
 = 3000 kPa
= 3000 kPa
turbine temperature at the inlet
 = ( -160+273)K = 113K
= ( -160+273)K = 113K
The pressure at the turbine exit
 = 300 kPa
= 300 kPa
Power produced by the turbine W = 120 kW
Density of LNG
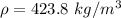
The formula for the workdone by an ideal turbine can be expressed by:
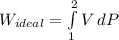
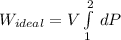
![W_(ideal) ={V} [P]^2_(1)](https://img.qammunity.org/2021/formulas/engineering/college/y0szeomouc7xa5urot78pq7tgvs7614aiq.png)
![W_(ideal) ={V} [P_1-P_2]](https://img.qammunity.org/2021/formulas/engineering/college/7m10778ncn2i1rlh2dty4r79od9gvnoai3.png)
We all know that density = mass * volume i.e
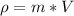
Then ;
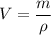
replacing it into the above previous derived formula; we have:
![W_(ideal) ={ (m)/(\rho)} [P_1-P_2]](https://img.qammunity.org/2021/formulas/engineering/college/ztdvg5qcl6kgotwj32j5h2pl2e3srb20pl.png)
![W_(ideal) ={ (20)/(423.8)} [3000-300]](https://img.qammunity.org/2021/formulas/engineering/college/e7nu5ofufp5q8iexcugnq0mcvhru96lk63.png)
![W_(ideal) ={ (20)/(423.8)} [2700]](https://img.qammunity.org/2021/formulas/engineering/college/rclzfr6ign4nosi1thpoli7js4ba1eeb2s.png)
![W_(ideal) =0.04719*[2700]](https://img.qammunity.org/2021/formulas/engineering/college/9kpdcv3pg9n9g9518e831kaafxk4jvrflq.png)
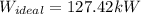
However ; the isentropic efficiency of turbine is given by the relation:
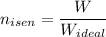
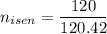
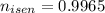
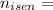 99.65%
99.65%
Therefore, the isentropic efficiency of turbine is 99.65%