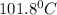Question

An ethylene glycol solution contains 21.4 g of ethylene glycol (C2H6O2) in 97.6 mL of water. (Assume a density of 1.00 g/mL for water.) Determine the freezing point and boiling point of the solution. (Assume a density of 1.00 g/ mL for water.)

Answer 1

Answer: The freezing point and boiling point of the solution are
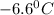`-6.6^0C` and
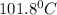`101.8^0C` respectively.

Step-by-step explanation:

Depression in freezing point:

`T_f^0-T^f=i* k_f* (w_2* 1000)/(M_2* w_1)`

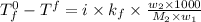
where,

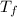`T_f` = freezing point of solution = ?

`T^o_f` = freezing point of water =
`0^0C`

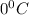
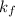`k_f` = freezing point constant of water =
`1.86^0C/m`

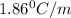
i = vant hoff factor = 1 ( for non electrolytes)

m = molality

`w_2` = mass of solute (ethylene glycol) = 21.4 g

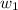`w_1`= mass of solvent (water) =
`density* volume=1.00g/ml* 97.6ml=97.6g`

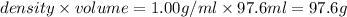
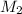`M_2` = molar mass of solute (ethylene glycol) = 62g/mol

Now put all the given values in the above formula, we get:

`(0-T_f)^0C=1* (1.86^0C/m)* ((21.4g)* 1000)/(97.6g* (62g/mol))`

`T_f=-6.6^0C`

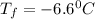
Therefore,the freezing point of the solution is
`-6.6^0C`

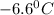
Elevation in boiling point :

`T_b-T^b^0=i* k_b* (w_2* 1000)/(M_2* w_1)`

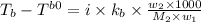
where,

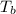`T_b` = boiling point of solution = ?

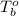`T^o_b` = boiling point of water =
`100^0C`

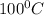
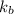`k_b` = boiling point constant of water =
`0.52^0C/m`

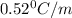
i = vant hoff factor = 1 ( for non electrolytes)

m = molality

`w_2` = mass of solute (ethylene glycol) = 21.4 g

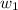`w_1`= mass of solvent (water) =
`density* volume=1.00g/ml* 97.6ml=97.6g`

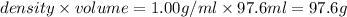
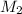`M_2` = molar mass of solute (ethylene glycol) = 62g/mol

Now put all the given values in the above formula, we get:

`(T_b-100)^0C=1* (0.52^0C/m)* ((21.4g)* 1000)/(97.6g* (62g/mol))`

`T_b=101.8^0C`

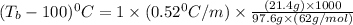
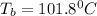
Thus the boiling point of the solution is
`101.8^0C`