Question

A hot air balloon is used as an air-vehicle to carry passengers. It is assumed that this balloon is sealed and has a spherical shape. Initially, the balloon is filled up with air at the pressure and temperature of 100 kPa and 27°C respectively and the initial diameter (D) of the balloon is 10 m. Then the balloon is heated up to the point that the volume is 1.2 times greater than the original volume (V2 =1.2V1 ). Due to elastic material used in this balloon, the inside pressure ( P ) is proportional to balloonâs diameter, i.e. P = ð¼D, where ð¼ is a constant.

Required:
a. Show that the process is polytropic (i.e. PV" = Constant) and find the exponent n and the constant.
b. Find the temperature at the end of the process by assuming air to be ideal gas.
c. Find the total amount of work that is done by the balloon's boundaries and the fraction of this work that is done on the surrounding atmospheric air at the pressure of 100 kPa.

Answer 1

a.
`(D_(1))/( D_(2)) = \left (\frac{ \left{D_1} }{ {D_2}} \right )^(-3* n)` which is constant therefore, n = constant

b. The temperature at the end of the process is 109.6°C

c. The work done by the balloon boundaries = 10.81 MJ

The work done on the surrounding atmospheric air = 10.6 MJ

Step-by-step explanation:

p₁ = 100 kPa

T₁ = 27°C

D₁ = 10 m

v₂ = 1.2 × v₁

p ∝ α·D

α = Constant

`v_1 = (4)/(3) * \pi * r^3`

`\therefore v_1 = (4)/(3) * \pi * \left ((10)/(2) \right )^3 = 523.6 \ m^3`

v₂ = 1.2 × v₁ = 1.2 × 523.6 = 628.32 m³

Therefore, D₂ = 10.63 m

We check the following relation for a polytropic process;

`(p_(1))/(p_(2)) = \left ((V_(2))/(V_(1)) \right )^(n) = \left ((T_(1))/(T_(2)) \right )^{(n)/(n-1)}`

We have;

`(\alpha * D_(1))/(\alpha * D_(2)) = \left (( (4)/(3) * \pi * \left ((D_2)/(2) \right )^3)/((4)/(3) * \pi * \left ((D_1)/(2) \right )^3) \right )^(n) = \left (\frac{ \left{D_2} ^3}{ {D_1}^3} \right )^(n)`

`(D_(1))/( D_(2)) = \left (\frac{ \left{D_2} }{ {D_1}} \right )^(3* n) = \left (\frac{ \left{D_1} }{ {D_2}} \right )^(-3* n)`

`( D_(1))/( D_(2)) = \left ( 1.2 \right )^(n) = \left (\frac{ \left{D_2} ^3}{ {D_1}^3} \right )^(n)`

`log \left ((D_(1))/( D_(2))\right ) = -3* n * log\left (\frac{ \left{D_1} }{ {D_2}} \right )`

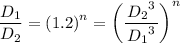
n = -1/3

Therefore, the relation, pVⁿ = Constant

b. The temperature T₂ is found as follows;

`\left ((628.32 )/(523.6) \right )^{-(1)/(3) } = \left ((300.15)/(T_(2)) \right )^{(-(1)/(3))/(-(1)/(3)-1)} = \left ((300.15)/(T_(2)) \right )^{(1)/(4)}`

T₂ = 300.15/0.784 = 382.75 K = 109.6°C

c.
`W_(pdv) = (p_1 * v_1 -p_2 * v_2 )/(n-1)`

`p_2 = (p_(1))/( \left ((V_(2))/(V_(1)) \right )^(n) ) = \frac{100* 10^3}{ \left (1.2) \right ^{-(1)/(3) } }`

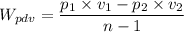
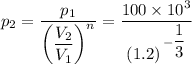
p₂ = 100000/0.941 = 106.265 kPa

`W_(pdv) = (100 * 10^3 * 523.6 -106.265 * 10^3 * 628.32 )/(-(1)/(3) -1) = 10806697.1433 \ J`

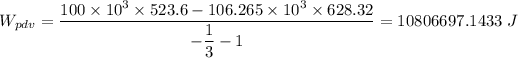
The work done by the balloon boundaries = 10.81 MJ

Work done against atmospheric pressure, Pₐ, is given by the relation;

Pₐ × (V₂ - V₁) = 1.01×10⁵×(628.32 - 523.6) = 10576695.3 J

The work done on the surrounding atmospheric air = 10.6 MJ