Answer and Explanation:
For computing the initial quantity of helium we have to apply the law of ideal gas which is shown below:
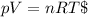
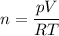
Now we have to compute the ratio between the initial and the final numbers of moles which is
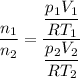
The statement defines that
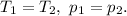
Therefore
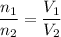
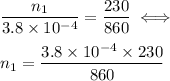
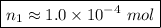
And, the variables are known is starting volume and ending gas quantity