Question

The yield strength for an alloy that has an average grain diameter, d1, is listed above as Yield Stress 1 . At a grain diameter of d2, the yield strength increases Yield Stress 2. At what grain diameter, in mm, will the yield strength be 217 MPa

Answer 1

Complete Question:

Grain diameter 1 (mm) = 4.4E-02

Yield stress 1 (MPa) = 131

Grain diameter 2 (mm) = 7.7E-03

Yield Stress 2 (MPa) = 268

The yield strength for an alloy that has an average grain diameter, d1, is listed above as Yield Stress 1 . At a grain diameter of d2, the yield strength increases Yield Stress 2. At what grain diameter, in mm, will the yield strength be 217 MPa

Answer:

d = 1.3 * 10⁻² m

Step-by-step explanation:

According to the Hall Petch equation:

`\sigma_y = \sigma_0 + k/√(d) \\`

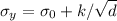
At
`d_(1) = 4.4 * 10^(-2) mm`,
`\sigma_(y1) = 131 MPa = 131 N/ mm^2`

`131 = \sigma_0 + k/\sqrt{4.4 * 10^(-2)} \\k = 27.45 - 0.2096 \sigma_0`

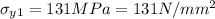
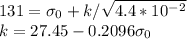
At
`d_(2) = 7.7 * 10^(-3) mm`,
`\sigma_(y2) = 131 MPa = 268 N/ mm^2`

`268 = \sigma_0 + (27.45 - 0.2096 \sigma_0)/\sqrt{7.7 * 10^(-3)} \\23.5036 = 27.47 - 0.1219 \sigma_0\\ \sigma_0 = 32.45 N/mm^2`

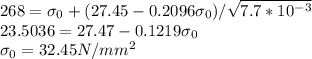
k = 27.45 - 0.2096(32.45)

k = 20.64

At
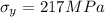`\sigma_y = 217 MPa`, reapplying Hall Petch law:

`\sigma_y = \sigma_0 + k/√(d) \\`

`217 =32.45 + 20.64/√(d) \\217 - 32.45 = 20.64/√(d)\\184.55 = 20.64/ √(d) \\√(d) = 20.64/184.55\\√(d) = 0.11184\\d = 0.013 mm`

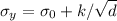
d = 1.3 * 10⁻² m