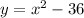Question

Write the quadratic equation whose roots are -6 and 6, and whose leading coefficient is 1 .

Answer 1

The quadratic equation is:
`y=x^2-36`

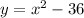
Explanation:

If the roots of the quadratic equation are "-6" and "6", then it must have the following factors:
`(x+6)\,\, and \,\,(x-6)`

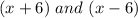
Therefore, we can write the equation in factor form as:

`y=a\,(x+6)\,(x-6)`

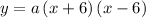
where a is a real number constant factor. Now, this equation in standard form will look like:

`y=a\,(x^2+6x-6x-6^2)=a\,(x^2-36)=ax^2-36\,a`

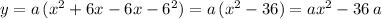
Therefore, using the information about the leading coefficient being "1" (one), we derive that the constant factor
`a` must be "1". The final expression for the quadratic becomes:

`y=x^2-36`