Question

A 50-loop circular coil has a radius of 3 cm. It is oriented so that the field lines of a magnetic field are perpendicular to the coil. Suppose that the magnetic field is varied so that B increases from 0.10 T to 0.35 T in 2 ms. Find the induced emf in the coil.

Answer 1

-17.8 V

Step-by-step explanation:

The induced emf in a coil is given as:

`E = (-NdB\pi r^2)/(dt)`

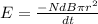
where N = number of loops

dB = change in magnetic field

r = radius of coil

dt = elapsed time

From the question:

N = 50

dB = final magnetic field - initial magnetic field

dB = 0.35 - 0.10 = 0.25 T

r = 3 cm

dt = 2 ms = 0.002 secs

Therefore, the induced emf is:

`E = (-50 * 0.25 * \pi * 0.03^2)/(0.002) \\E = -17.8 V`

Note: The negative sign implies that the EMf acts in an opposite direction to the change in magnetic flux.