Question

Fifty random shoppers at an electronics store have been interviewed and 35 of them intend to purchase a newly released smart phone. What probability distribution describes this situation and what are its mean and standard deviation of phone sales if we are concerned about 1071 shoppers that day

Answer 1

We use the binomial distribution to describe this situation.

The mean number of phone sales is 749.7 with a standard deviation of 15.

Explanation:

For each shopper, there are only two possible outcomes. Either they plan to purchase the newly released smart phone, or they do not. Each customer is independent of other customers. So we use the binomial distribution to solve this question.

Binomial probability distribution

Probability of exactly x sucesses on n repeated trials, with p probability.

The expected value of the binomial distribution is:

`E(X) = np`

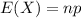
The standard deviation of the binomial distribution is:

`√(V(X)) = √(np(1-p))`

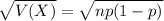
Fifty random shoppers at an electronics store have been interviewed and 35 of them intend to purchase a newly released smart phone.

This means that
`p = (35)/(50) = 0.7`

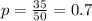
What are its mean and standard deviation of phone sales if we are concerned about 1071 shoppers that day

1071 shoppers, so
`n = 1071`

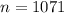
Mean

`E(X) = 1071*0.7 = 749.7`

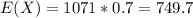
Standard deviation

`√(V(X)) = √(1071*0.7*0.3) = 15`

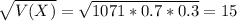
The mean number of phone sales is 749.7 with a standard deviation of 15.