Answer:
Width = 4 units
Explanation:
Let us pose the width as w, and the length as l. If the length is 2 units greater than the width, consider the following;
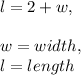
The area of this rectangle can be determined through length * width / l * w, and is given to be 24 square units. We can say l = 2 + w instead, solving for the width ( w );
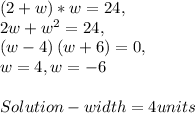
As the width couldn't be a negative value, we had to take the positive of 4 and - 6, which was 4 units.