Question

In a study of the effectiveness of airbags in cars, 11,541 occupants were observed in car crashes with airbags available, and 41 of them were fatalities. Among 9,853 occupants in crashes with airbags not available, 52 were fatalities. (a) Construct a 95% confidence interval for the difference of the two population fatality rates. (please keep 4 decimal places throughout for accuracy) (b) Based on the confidence interval

Answer 1

Please the read the answer below

Explanation:

In order to find the 95% confidence interval for the difference of the two populations, you use the following formula (which is available when the population size is greater than 30):

CI =
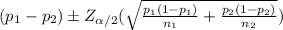`(p_1-p_2)\pm Z_(\alpha/2)(\sqrt{(p_1(1-p_1))/(n_1)+(p_2(1-p_2))/(n_2)})` (1)

where:

p1: proportion of one population = 52/9853 = 0.0052

p2: proportion of the other population = 41/11541 = 0.0035

α: tail area = 1 - 0.95 = 0.05

Z_α/2: Z factor of normal distribution = Z_0.025 = 1.96

n1: sample of the first population = 52

n2: sample of the second population = 41

You replace the values of all parameters in the equation (1) :

`CI =(0.0052-0.0035)\pm (1.96)(\sqrt{(0.0052(1-0.0052))/(52)+(0.0035(1-0.0035))/(41)})\\\\CI=0.0017\pm0.026`

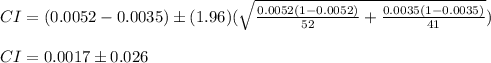
By the result obtained in the solution, you can conclude that the sample is not enough, because the margin error is greater that the difference of proportion of each sample population.