Question

A satellite in the shape of a solid sphere of mass 1,900 kg and radius 4.6 m is spinning about an axis through its center of mass. It has a rotation rate of 8.0 rev/s. Two antennas deploy in the plane of rotation extending from the center of mass of the satellite. Each antenna can be approximated as a rod of mass 150.0 kg and length 6.6 m. What is the new rotation rate of the satellite (in rev/s)

Answer 1

Therefore, the new rotation rate of the satellite is 6.3 rev/s.

Step-by-step explanation:

The expression for conservation of the angular momentum (L) is

`L_(i) = L_(f) I_(i)*\omega_(i) = I_(f)*\omega_(f)`

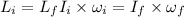
Where

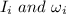`I_(i)\ and \ \omega_(i)` initial moment of inertia and angular velocity

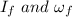`I_(f)\ and \ \omega_(f)` is the final moment of inertia and angular velocity

The expression of moment of inertia of the satellite (a solid sphere) is

`I_(i) = (2)/(5)m_(s)r^(2)`

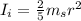
Where
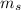`m_(s)` is the satellite mass

r is the radus of the sphere

Substititute 1900kg for m and 4.6m for r

`I_(i) = (2)/(5)m_(s)r^(2)\\\\ = (2)/(5)*1900 kg* (4.6 m)^(2) \\\\= 1.61 \cdot 10^(4) kgm^(2)`

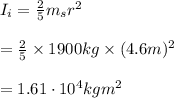
The final moment of inertia of the satellite about the centre of mass

`I_(f) = I_(i) + 2*I_(x) \\\\= 1.61 \cdot 10^(4) kgm^(2) + 2*(1)/(3)m_(x)l^(2)`

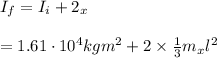
Where
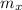`m_(x)` is the antenna's mass and

I is the length of the antenna

`I_(f) = 1.61 \cdot 10^(4) kgm^(2) + 2*(1)/(3)150.0 kg*(6.6 m)^(2) \\\\= 2.05 \cdot 10^(4) kgm^(2)`

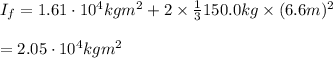
So, the Final rotation rate of the satellite is:

`I_(i)*\omega_(i) = I_(f)*\omega_(f) \\\\\omega_(f) = (I_(i)*\omega_(i))/(I_(f)) \\\\= (1.61 \cdot 10^(4) kgm^(2)*8.0 (rev)/(s))/(2.05 \cdot 10^(4) kgm^(2)) \\\\= 6.3 rev/s`

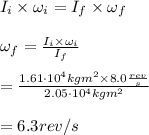
Therefore, the new rotation rate of the satellite is 6.3 rev/s.