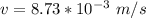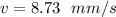Here is the complete question.
The cylinder contains mw = 1.80 kg of water at just under 100°C. The piston has a radius of r = 6.35 cm, mass of mp = 2.70 kg, and initially rests on the surface of the water. The heater transfers energy to the water at the rate of 150 W. The latent heat of vaporization of water is Lvap = 2.26 ✕ 106 J/kg, and the specific heat of steam is csteam = 2,010 J/(kg ° C). The top of the piston is exposed to atmospheric pressure.
Once the water begins boiling, how fast does the piston rise ( in mm/s)?
Answer:
thus, once the water begins boiling, the speed of the piston rise is 8.73 mm/s
Explanation:
Given that:
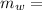 1.80 kg
1.80 kg
radius r = 6.35 cm
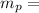 2.70 kg
2.70 kg
rate of energy transfer = 150 W
latent heat of vaporization of water

specific heat of steam is
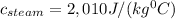
From the given information;
the speed rise of the piston can be perceived to be of the same rate at which the height of the steam above the water is also increasing due to boiling.
Thus; volume of the gas
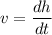
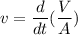
Using the ideal gas law to replace the volume of the gas where the pressure and temperature are constant: we have;

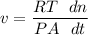
However; the number of moles n in the mass
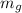 of the gas to the molecular mass
of the gas to the molecular mass
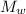 is ;
is ;
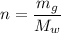
Replacing that into the above velocity formulae; we have:
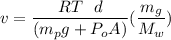
where F = PA and F is the product of atmospheric pressure and area of piston plus the weight of the piston; i.e
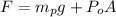
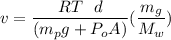
/(dt))](https://img.qammunity.org/2021/formulas/mathematics/college/36axsd8qx10sfv0ssy6ikqo22ifvagtrz6.png)
where;
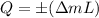
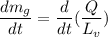
Again;
/(dt))((Q)/(L_v))](https://img.qammunity.org/2021/formulas/mathematics/college/hlvollcvialk6ygublr2z93bkalyqnkqq3.png)
/(dt))](https://img.qammunity.org/2021/formulas/mathematics/college/p8528hnriedzv9dclgtm44zratii4kdd9n.png)
![v =[(RT \ \ Power)/((m_pg+ P_oA)M_w * L_v)]](https://img.qammunity.org/2021/formulas/mathematics/college/ryyebqyt2im3bdrhi2cbta7v4osb8g6ian.png)
![v =[((8.314*373)(150))/(((2.70*9.8)+ (1.013*10^5)(\pi*0.0635^2))(0.0180 * 2.26*10^6)]](https://img.qammunity.org/2021/formulas/mathematics/college/ln2tkh3tjccgjg2200t87ffhnvbhtebjj0.png)