Question

Two blocks of rubber (B) with a modulus of rigidity G = 14 MPa are bonded to rigid supports and to a rigid metal plate A. Knowing that c = 80 mm and P = 46 kN, determine the smallest allowable dimensions a and b of the blocks if the shearing stress in the rubber is not to exceed 1.4 MPa and the deflection of the plate is to be at least 7 mm.

Answer 1

a = 0.07m or 70mm

b = 0.205m or 205mm

Step-by-step explanation:

Given the following data;

Modulus of rigidity, G = 14MPa=14000000Pa.

c = 80mm = 0.08m.

P = 46kN=46000N.

Shearing stress (r) in the rubber shouldn't exceed 1.4MPa=1400000Pa.

Deflection (d) of the plate is to be at least 7mm = 0.007m.

From shearing strain;

[

`Modulus Of Elasticity, E = (d)/(a) =(r)/(G)`

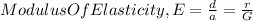
Making a the subject formula;

`a = (Gd)/(r)`

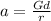
Substituting into the above formula;

`a = (14000000*0.007)/(1400000)`

`a = (98000)/(1400000)`

`a = 0.07m or 70mm`

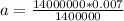
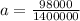
a = 0.07m or 70mm.

Also, shearing stress;

`r = (P)/(2bc)`

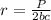
Making b the subject formula;

`b = (P)/(2cr)`

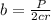
Substituting into the above equation;

`b = (46000)/(2*0.08*1400000)`

`b = (46000)/(224000)`

`b = 0.205m or 205mm`

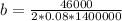
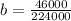
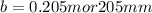
b = 0.205m or 205mm