Answer:
B. The endpoint of the dilated line is (-2,4),(6,8)
Explanation:
Given
Line segment AB
Endpoints: A(-3,6) and B(9,12)
Scale Factor: 2/3 about the origin
Required
Find the end points of the dilated line
From the question, we understand that the line segment is dilated about the origin;
The keywords about the origin implies that, to get the endpoints of the dilated line, we simply multiply the coordinates of of the original line by the scale factor;
This is shown below;
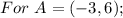
The new endpoints become
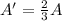

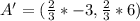

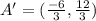
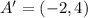
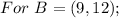
The new endpoints become
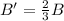
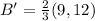
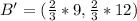
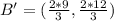
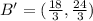
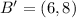
Hence, the endpoint of the dilated line is (-2,4),(6,8)