Question

g Question 6 1 pts A 3x3 matrix with real entries can have (select ALL that apply) Group of answer choices three eigenvalues, all of them real. three eigenvalues, all of them complex. two real eigenvalues and one complex eigenvalue. one real eigenvalue and two complex eigenvalues. only two eigenvalues, both of them real. only two eigenvalues, both of them complex. only one eigenvalue -- a real one. only one eigenvalue -- a complex one.

Answer 1

(A)three eigenvalues, all of them real.

(D)one real eigenvalue and two complex eigenvalues.

(G)only one eigenvalue -- a real one.

Explanation:

Given an
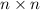`n * n` matrix, the characteristic polynomial of the matrix is the degree n polynomial in one variable λ:

`p(\lambda) = det(\lambda I- A)`

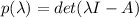
If such
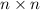`n * n` matrix A has real entries, its complex eigenvalues will always occur in complex conjugate pairs.

Therefore, for a
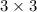`3 * 3` matrix with real entries, the following are possible:

(A)three eigenvalues, all of them real.

(D)one real eigenvalue and two complex eigenvalues.

(G)only one eigenvalue -- a real one.

A
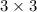`3 * 3` matrix with real entries cannot have the following:

(B)three eigenvalues, all of them complex.

(C)two real eigenvalues and one complex eigenvalue.

(E)only two eigenvalues, both of them real.

(F)only two eigenvalues, both of them complex.

(H)only one eigenvalue -- a complex one.