Question

John is putting a fence around his garden that is shaped like a half circle and a rectangle. A rectangle has a length of 14 feet and width of 7 feet. A semicircle with diameter of 7 feet is on top of the rectangle. How much fencing will John need? Use StartFraction 22 over 7 EndFraction for Pi. 32 ft 39 ft 46 ft 57 ft

Answer 1

46

Explanation:

Answer 2

He needs approximately 46 feet of fencing.

Explanation:

John's garden has a shape of a composite figure as shown in the annexed drawing. To find the length of the fencing he needs we need to find the perimeter of the rectangle and subtract it with the width and find the length of the circle and divide it by two. This is done below:

`\text{fence} = (\text{rectangle perimeter} - \text{width}) + (\frac{\text{circle perimeter}}{2})\\\text{fence} = (2*14 + 2*7 - 7) + ((2*\pi*3.5)/(2))\\\text{fence} = 35 + 11 = 46 \text{ feet}`

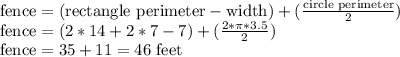
He needs approximately 46 feet of fencing.