Question

If a tank holds 4500 gallons of water, which drains from the bottom of the tank in 50 minutes, then Toricelli's Law gives the volume V of water remaining in the tank after t minutes as V = 4500 1 − 1 50 t 2 0≤ t ≤ 50. Find the rate at which water is draining from the tank after the following amounts of time.a) 5 min 855 x gal/min b) 10 min 160 x gal/min c) 20 min 120 x gal/min d) 50 min gal/min

Answer 1

a) at 5 minutes: 162 gal/min

b) at 10 minutes: 144 gal/min

c) at 20 minutes: 108 gal/min

d) at 50 minutes: 0 gal/min

Explanation:

Considering the formula given by the volume of water remaining in the tank:

`V(t)=4500\,(1-(1)/(50) \,t)^2`

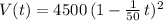
we can find the rate of water draining from the tank, (that is change in volume divided elapsed time) with the derivative of the function at the different times. Notice that this function has a decaying curvature (see attached image) of volume as a function of time, and the idea is therefore to find the slope of the tangent line at the different requested times.

So we first calculate the derivative of this function at any time 't":

`V(t)=4500\,(1-(1)/(50) \,t)^2\\V'(t)=9000\,(1-(1)/(50) \,t)\,(-(1)/(50))\\V'(t)=-180(1-(1)/(50) \,t)\\V'(t)=-180+3.6\,t`

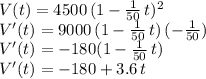
And now we estimate this derivative at the different requested points for time values:

a) at 5 minutes:
`V'(5)=-180+3.6\,(5) = -162\,\,gal/min`

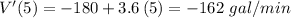
b) at 10 minutes:
`V'(10)=-180+3.6\,(10) = -144\,\,gal/min`

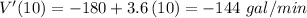
c) at 20 minutes:
`V'(20)=-180+3.6\,(20) = -108\,\,gal/min`

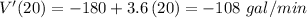
d) at 50 minutes:
`V'(50)=-180+3.6\,(50) = 0\,\,gal/min`

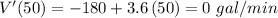
All the negative signs preceding indicate that the remaining volume in the tank is reducing as time goes by, so the volume at which the water is draining is actually the absolute value of those numbers.