Question

Using a 685 nm wavelength laser, you form the diffraction pattern of a 1.11 mm wide slit on a screen. You measure on the screen that the 11th dark fringe is 9.85 cm away from the center of the central maximum. How far is the screen located from the slit

Answer 1

13.8 m

Step-by-step explanation:

Dark fringes are formed in a single slit experiment due to destructive interference that occurs due to interference.

The position of these dark fringes formed on a screen is given by:

`y = (\lambda )/(d) (m + 1/2)D`

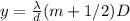
where y = position of mth minimum

m = order of the minimum

D = distance of the slit from the screen

d = width of the slit

λ = wavelength of the light used

We need to find D:

`D = \frac{yd} {\lambda (m + 1/2)} \\`

From the question:

m = 11

y = 9.85 cm = 0.0985 m

λ =
`6.83 * 10^(-7) m`

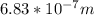
d = 1.11 mm = 0.0011 m

Therefore:

`D = \frac{0.0985 *0.0011} {6.83 * 10^(-7) *(11 + 1/2)} \\\\D = \frac{0.00010835} {6.83 * 10^(-7) * (23/2)} \\\\D = 13.8 m`

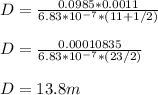
The slit is 13.8 m far from the screen