Answer:
For the statement;
If M is the midpoint of
 , then
, then
 is congruent to
is congruent to
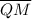
The contrapositive statement is therefore;
If M is not the midpoint of
 , then
, then
 is not congruent to
is not congruent to
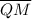
Explanation:
Contraposition in logic describes the transitioning from an implication/conditional statement into its equivalent contrapositive
The contrapositive of the statement p → q is equal to ~p → ~q
Therefore, the contrapositive of a conditional or implication statement is equivalent, logically to the original statement