Answer:
75.76% probability that there will be 10 or more customers at this bank in one hour.
Explanation:
In a Poisson distribution, the probability that X represents the number of successes of a random variable is given by the following formula:

In which
x is the number of sucesses
e = 2.71828 is the Euler number
 is the mean in the given interval.
is the mean in the given interval.
A bank gets an average of 12 customers per hour.
This means that
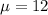
Find the probability that there will be 10 or more customers at this bank in one hour.
Either there are less than 10 customers, or there are 10 or more. The sum of the probabilities of these events is 1. Then
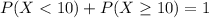
We want

Then
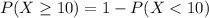
In which

So

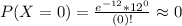
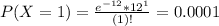

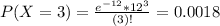
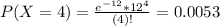

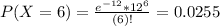
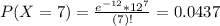
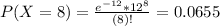
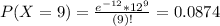
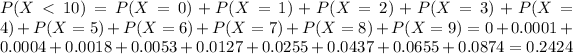
Then
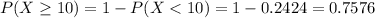
75.76% probability that there will be 10 or more customers at this bank in one hour.