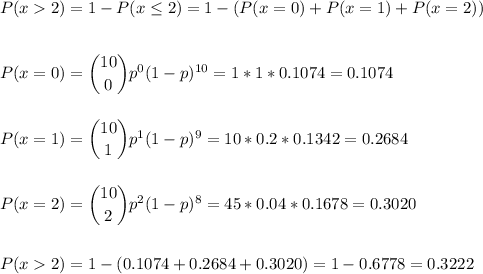Question

Gears produced by a grinding process are categorized either as conforming (suitable for their intended purpose), downgraded (unsuitable for the intended purpose but usable for another purpose), or scrap (not usable). Suppose that 80% of the gears produced are conforming, 15% are downgraded, and 5% are scrap. Ten gears are selected at random. A. What is the probability that one or more is scrap?B. What is the probability that eight or more are not scrap?C. What is the probability that more than two are degraded or scarp?

Answer 1

A. P=0.4013

B. P=0.9884

C. P=0.3222

Explanation:

We can model this with a binomial random variable.

The sample size is n=10.

The probability is p=0.05 for scrap and p=0.05+0.15=0.20 for degraded or scrap.

The probability of having k scrap gears in the sample is:

`P(x=k) = \dbinom{n}{k} p^(k)(1-p)^(n-k)\\\\\\P(x=k) = \dbinom{10}{k} 0.05^(k) 0.95^(10-k)\\\\\\`

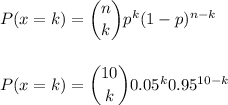
The probability that one or more is scrap can be calculated as 100% less the probability that no one is scrap:

`P(x\geq1)=1-P(x=0)\\\\\\P(x=0) = \dbinom{10}{0} p^(0)(1-p)^(10)=1*1*0.5987=0.5987\\\\\\P(x\geq1)=1-0.5987=0.4013`

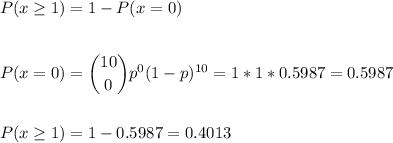
The probability that 8 or more are not scrap is equal to the probability of having 2 or less that are scrap:

`P(x\leq2)=P(x=0)+P(x=1)+P(x=2)\\\\\\P(x=0) = \dbinom{10}{0} p^(0)(1-p)^(10)=1*1*0.5987=0.5987\\\\\\P(x=1) = \dbinom{10}{1} p^(1)(1-p)^(9)=10*0.05*0.6302=0.3151\\\\\\P(x=2) = \dbinom{10}{2} p^(2)(1-p)^(8)=45*0.0025*0.6634=0.0746\\\\\\P(x\leq2)=0.5987+0.3151+0.0746=0.9884`

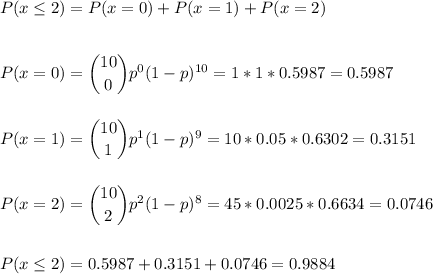
The probability that more than two are degraded or scrap (p=0.2) is calculated as:

`P(x>2)=1-P(x\leq2)=1-(P(x=0)+P(x=1)+P(x=2))\\\\\\P(x=0) = \dbinom{10}{0} p^(0)(1-p)^(10)=1*1*0.1074=0.1074\\\\\\P(x=1) = \dbinom{10}{1} p^(1)(1-p)^(9)=10*0.2*0.1342=0.2684\\\\\\P(x=2) = \dbinom{10}{2} p^(2)(1-p)^(8)=45*0.04*0.1678=0.3020\\\\\\P(x>2)=1-(0.1074+0.2684+0.3020)=1-0.6778=0.3222`